零知识证明： Tornado Cash 项目学习

2024-05-10 08:56:10

前言

最近在了解零知识证明方面的内容，这方面的内容确实不好入门也不好掌握，在了解了一些基础的概念以后，决定选择一个应用了零知识证明的项目来进行进一步的学习。最终选择了 Tornado Cash 这个项目，因为它著名且精致，适合入门的同学进行学习。

学习 Tornado Cash 项目，涉及以下方面：

了解项目功能与特性
了解项目智能合约实现
了解项目零知识证明部分实现

合约地址： https://etherscan.io/address/0x910cbd523d972eb0a6f4cae4618ad62622b39dbf#code

项目概览

Tornado Cash 项目的主要功能是代币混淆。由于区块链上所有的交易都是公开的，所有人都可以通过分析交易的内容来得知在这笔交易中，代币从哪些地址流向了哪些地址。而当你希望把你的代币从账户 A 转移到账户 B ，但是又不想被人分析出这两个账户之间存在着转账关系，这个时候你就需要用到 Tornado Cash （下称 tornado）的代币混淆功能。

Tornado的主要业务流程：

用户根据存款金额选择对应的匿名池，并将资金发送到智能合约。合约会在不暴露取款凭证的前提下记录这笔存款操作。然后存款资金会在匿名池中与其他来源的资金混合。最后，用户提供取款凭证，通过零知识证明的校验，匿名池会将代币发送给指定的地址。这样就完成了一次代币混淆了。

存款页面

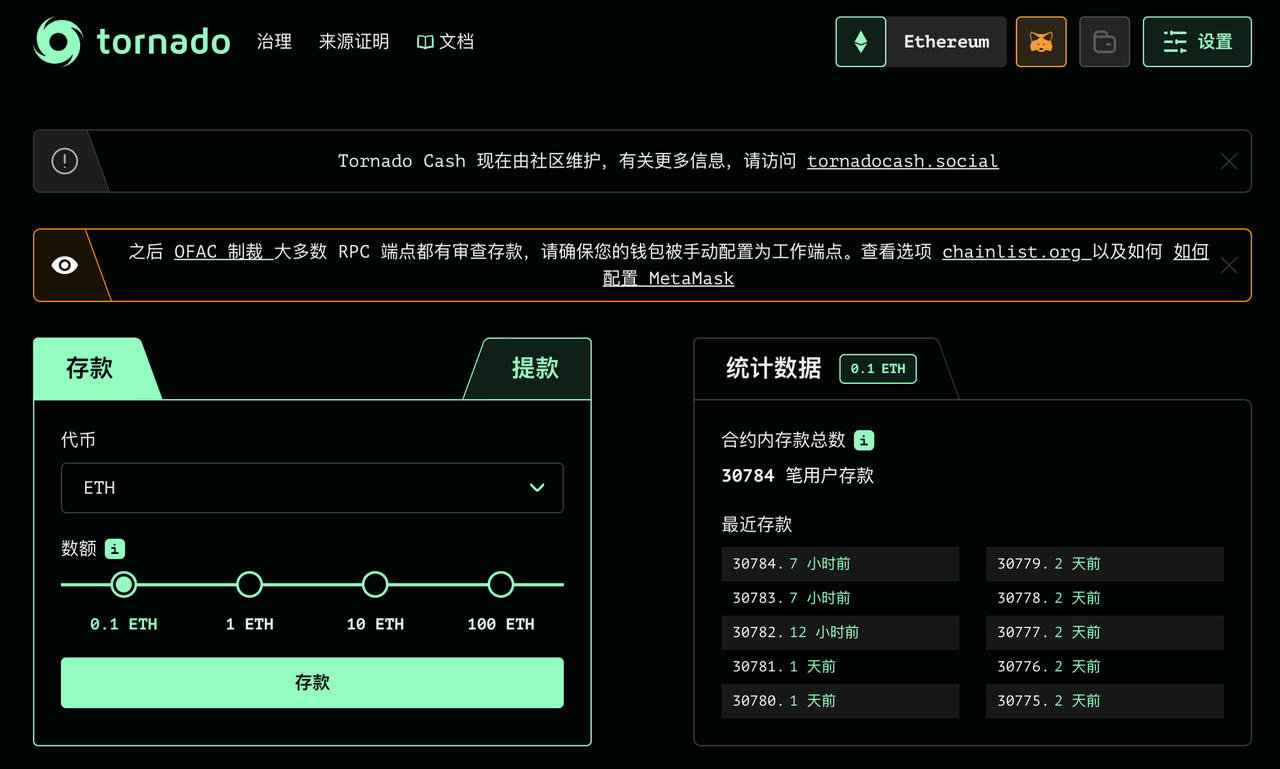
取款凭证

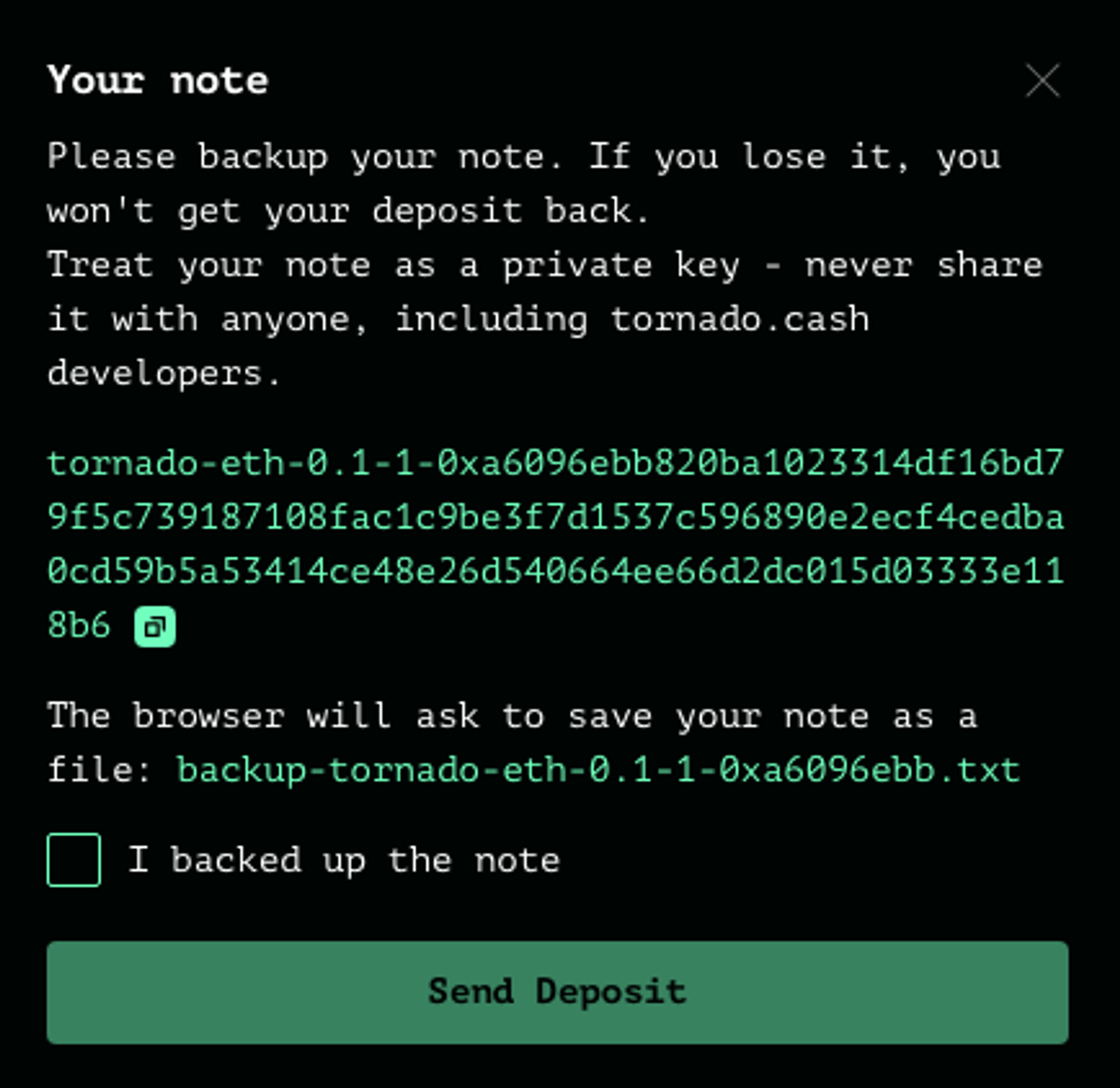
tornado-eth-0.1-1-0xa6096ebb820ba1023314df16bd79f5c739187108fac1c9be3f7d1537c596890e2ecf4cedba0cd59b5a53414ce48e26d540664ee66d2dc015d03333e118b6

提款页面

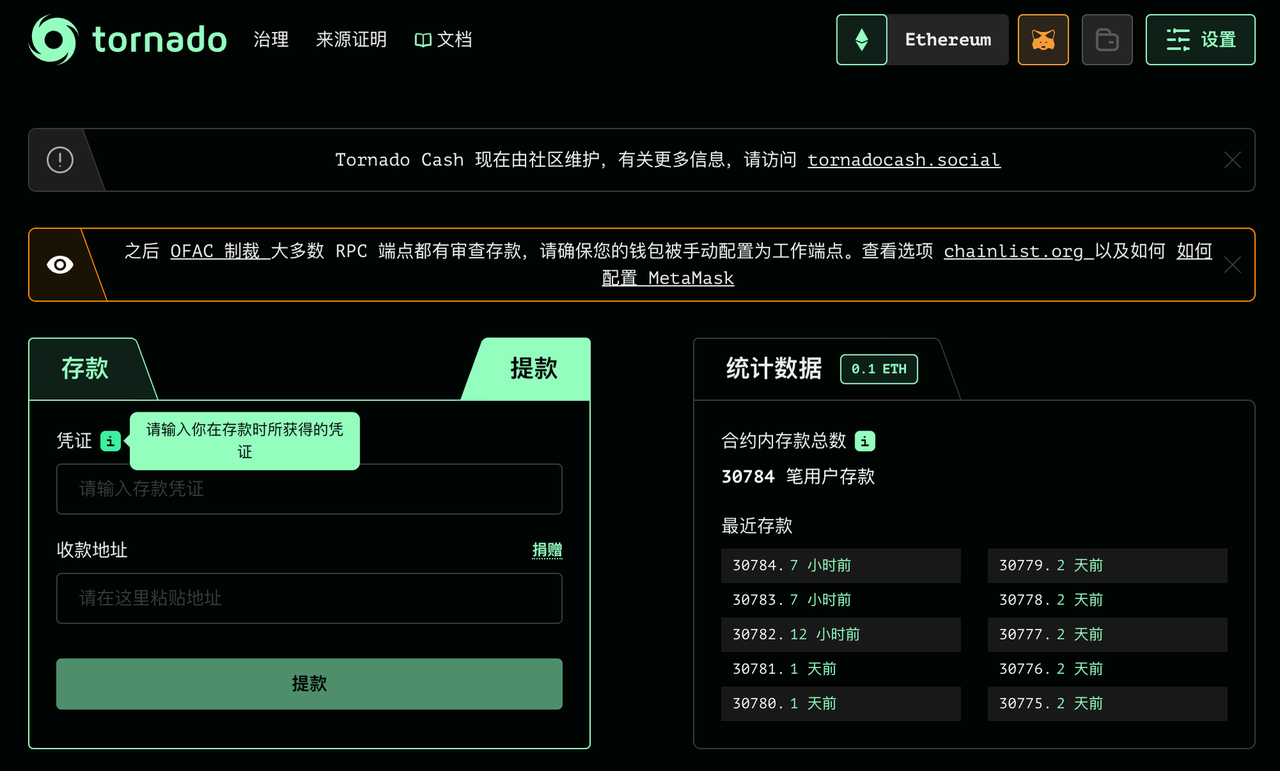
取款凭证所包含的信息

从 Tornado UI 代码中可以得知，当用户点击提款按钮时，将调用 onWithdraw 方法，该方法处理提款凭证的提交。

根据下面的代码流程，可以追溯到 note 的解析方法

components/withdraw/Withdraw.vue -> store/application.js -> utils/crypto.js

根据下面的代码，可以得知取款凭证被解析成以下内容

tornado(_) - 标识这是一个 Tornado Cash 的提款凭证。
eth(currency) - 加密货币的类型，这里是以太坊（ETH）。
0.1(amount) - 存款或提款的金额，这里是 0.1 ETH。
1(netId) - 网络ID，指示该凭证适用于哪个网络，如以太坊主网、Ropsten测试网等。
0xa609...e118b6(hexNote) - 加密的十六进制字符串，长度为 62 字节，是 nullifier 和 secret 的串联。

const CUT_LENGTH = 31

export function parseNote(note) {
  const [, currency, amount, netId, hexNote] = note.split('-')

  return {
    ...parseHexNote(hexNote),
    netId,
    amount,
    currency
  }
}

export function parseHexNote(hexNote) {
  const buffNote = Buffer.from(hexNote.slice(2), 'hex')

  const commitment = buffPedersenHash(buffNote)

  const nullifierBuff = buffNote.slice(0, CUT_LENGTH)
  const nullifierHash = BigInt(buffPedersenHash(nullifierBuff))
  const nullifier = BigInt(leInt2Buff(buffNote.slice(0, CUT_LENGTH)))

  const secret = BigInt(leInt2Buff(buffNote.slice(CUT_LENGTH, CUT_LENGTH * 2)))

  return {
    secret,
    nullifier,
    commitment,
    nullifierBuff,
    nullifierHash,
    commitmentHex: toFixedHex(commitment),
    nullifierHex: toFixedHex(nullifierHash)
  }
}

取款凭证的原像是两个值 ( nullifier + secret ) 的串联，产生长度为 62 字节的消息，前 31 字节为 Nullifier，后 31 字节为 Secret。

为什么是 31 个字节而不是 32 个字节？

从文档得知，采用的是 Baby Jubjub 椭圆曲线，该曲线在有限域 r = 21888242871839275222246405745257275088548364400416034343698204186575808495617 上。采用 31 字节的数字是为了能够使得所选择的 Nullifier 和 Secret 值都在有限域 r 内。

>>> 2 ** 248 < 21888242871839275222246405745257275088548364400416034343698204186575808495617
True
>>> 2 ** 256 < 21888242871839275222246405745257275088548364400416034343698204186575808495617
False

代码总览

整个 Tornado Cash 项目的核心代码主要分为 智能合约 和 约束电路 两部分。主要的业务逻辑包括存款和取款两个部分。

智能合约： https://github.com/tornadocash/tornado-core/tree/master/contracts
约束电路： https://github.com/tornadocash/tornado-core/tree/master/circuits

其中，存款部分与智能合约部分的业务逻辑相关，而取款部分与智能合约和约束电路两部分相关。

存款业务代码分析

Tornado 采用了一个高度 32 的默克尔树（Merkle tree）的叶子结点来存储存款信息，存储的最大数据量为 2 ** 32 。

调用 Tornado.deposit 函数进行存款，其中 _commitment 参数为两个秘密值拼接以后的哈希（ _commitment = hash(nullifier | secret) ）。

检查 _commitment 是否已经被使用了；
调用 _insert 函数把 _commitment 插入到树的叶子节点；
标记 _commitment 已经被使用了；
检查转入金额是否满足。

function deposit(bytes32 _commitment) external payable nonReentrant {
  require(!commitments[_commitment], "The commitment has been submitted");

  uint32 insertedIndex = _insert(_commitment);
  commitments[_commitment] = true;
  _processDeposit();

  emit Deposit(_commitment, insertedIndex, block.timestamp);
}

两种路径进行存款：

通过 Dap：参数由 Dapp 给你生成
直接调用智能合约：参数自己准备

这部分的代码逻辑比较简单，整个 Tornado 合约精妙的内容是在默克尔树的处理上，接下来我们进入到 MerkleTreeWithHistory 合约来进一步了解。

全局变量

在了解 MerkleTreeWithHistory 合约的业务逻辑之前，先来看一下它定义的全局变量。为了节省计算与存储成本，Tornado 采用了许多优化策略。下面的全局变量会在各个策略中使用，每个变量的含义如下：

// Baby Jubjub 椭圆曲线的有限域
// 同时也被应用在 MiMC 算法中，令所有输入输出值都需要进行 mod FIELD_SIZE 处理以确保落在有限域内。
uint256 public constant FIELD_SIZE = 21888242871839275222246405745257275088548364400416034343698204186575808495617;

// keccak256("tornado") % FIELD_SIZE 的值，用作填充未被使用的叶子节点。
uint256 public constant ZERO_VALUE = 21663839004416932945382355908790599225266501822907911457504978515578255421292;

// MIMC 哈希的实现合约，用字节码编写而成，没有 solidity 代码
IHasher public immutable hasher;

// 默克尔树树的高度，取值范围 (0, 32)
uint32 public levels;

// Merkle 树每个层级中最新更新的全使用的子树根节点，(层级 => 哈希值)。
mapping(uint256 => bytes32) public filledSubtrees;

// 每次更新后 Merkle 树根的值
mapping(uint256 => bytes32) public roots;

// 可以存储的最大树根数量，避免存储过多的历史信息
uint32 public constant ROOT_HISTORY_SIZE = 30;

// 当前 Merkle 树根的值，代表处于 (currentRootIndex / ROOT_HISTORY_SIZE) 的位置。
uint32 public currentRootIndex = 0;

// 下一个更新的叶子节点索引
uint32 public nextIndex = 0;

zeros() 预先计算空子树根节点的值

在 zeros 函数中，已经提前计算好了高度为 i 的每个空子树的根节点值。因为空叶子节点的值是固定的，所以可以提前计算出每个高度中，所有叶子节点都为空节点的子树的根。这样做可以节省大量的计算过程。

/// @dev provides Zero (Empty) elements for a MiMC MerkleTree. Up to 32 levels
function zeros(uint256 i) public pure returns (bytes32) {
  if (i == 0) return bytes32(0x2fe54c60d3acabf3343a35b6eba15db4821b340f76e741e2249685ed4899af6c);
  else if (i == 1) return bytes32(0x256a6135777eee2fd26f54b8b7037a25439d5235caee224154186d2b8a52e31d);
  else if (i == 2) return bytes32(0x1151949895e82ab19924de92c40a3d6f7bcb60d92b00504b8199613683f0c200);
  else if (i == 3) return bytes32(0x20121ee811489ff8d61f09fb89e313f14959a0f28bb428a20dba6b0b068b3bdb);
  else if (i == 4) return bytes32(0x0a89ca6ffa14cc462cfedb842c30ed221a50a3d6bf022a6a57dc82ab24c157c9);
  else if (i == 5) return bytes32(0x24ca05c2b5cd42e890d6be94c68d0689f4f21c9cec9c0f13fe41d566dfb54959);
  else if (i == 6) return bytes32(0x1ccb97c932565a92c60156bdba2d08f3bf1377464e025cee765679e604a7315c);
  else if (i == 7) return bytes32(0x19156fbd7d1a8bf5cba8909367de1b624534ebab4f0f79e003bccdd1b182bdb4);
  else if (i == 8) return bytes32(0x261af8c1f0912e465744641409f622d466c3920ac6e5ff37e36604cb11dfff80);
  else if (i == 9) return bytes32(0x0058459724ff6ca5a1652fcbc3e82b93895cf08e975b19beab3f54c217d1c007);
  else if (i == 10) return bytes32(0x1f04ef20dee48d39984d8eabe768a70eafa6310ad20849d4573c3c40c2ad1e30);
  else if (i == 11) return bytes32(0x1bea3dec5dab51567ce7e200a30f7ba6d4276aeaa53e2686f962a46c66d511e5);
  else if (i == 12) return bytes32(0x0ee0f941e2da4b9e31c3ca97a40d8fa9ce68d97c084177071b3cb46cd3372f0f);
  else if (i == 13) return bytes32(0x1ca9503e8935884501bbaf20be14eb4c46b89772c97b96e3b2ebf3a36a948bbd);
  else if (i == 14) return bytes32(0x133a80e30697cd55d8f7d4b0965b7be24057ba5dc3da898ee2187232446cb108);
  else if (i == 15) return bytes32(0x13e6d8fc88839ed76e182c2a779af5b2c0da9dd18c90427a644f7e148a6253b6);
  else if (i == 16) return bytes32(0x1eb16b057a477f4bc8f572ea6bee39561098f78f15bfb3699dcbb7bd8db61854);
  else if (i == 17) return bytes32(0x0da2cb16a1ceaabf1c16b838f7a9e3f2a3a3088d9e0a6debaa748114620696ea);
  else if (i == 18) return bytes32(0x24a3b3d822420b14b5d8cb6c28a574f01e98ea9e940551d2ebd75cee12649f9d);
  else if (i == 19) return bytes32(0x198622acbd783d1b0d9064105b1fc8e4d8889de95c4c519b3f635809fe6afc05);
  else if (i == 20) return bytes32(0x29d7ed391256ccc3ea596c86e933b89ff339d25ea8ddced975ae2fe30b5296d4);
  else if (i == 21) return bytes32(0x19be59f2f0413ce78c0c3703a3a5451b1d7f39629fa33abd11548a76065b2967);
  else if (i == 22) return bytes32(0x1ff3f61797e538b70e619310d33f2a063e7eb59104e112e95738da1254dc3453);
  else if (i == 23) return bytes32(0x10c16ae9959cf8358980d9dd9616e48228737310a10e2b6b731c1a548f036c48);
  else if (i == 24) return bytes32(0x0ba433a63174a90ac20992e75e3095496812b652685b5e1a2eae0b1bf4e8fcd1);
  else if (i == 25) return bytes32(0x019ddb9df2bc98d987d0dfeca9d2b643deafab8f7036562e627c3667266a044c);
  else if (i == 26) return bytes32(0x2d3c88b23175c5a5565db928414c66d1912b11acf974b2e644caaac04739ce99);
  else if (i == 27) return bytes32(0x2eab55f6ae4e66e32c5189eed5c470840863445760f5ed7e7b69b2a62600f354);
  else if (i == 28) return bytes32(0x002df37a2642621802383cf952bf4dd1f32e05433beeb1fd41031fb7eace979d);
  else if (i == 29) return bytes32(0x104aeb41435db66c3e62feccc1d6f5d98d0a0ed75d1374db457cf462e3a1f427);
  else if (i == 30) return bytes32(0x1f3c6fd858e9a7d4b0d1f38e256a09d81d5a5e3c963987e2d4b814cfab7c6ebb);
  else if (i == 31) return bytes32(0x2c7a07d20dff79d01fecedc1134284a8d08436606c93693b67e333f671bf69cc);
  else revert("Index out of bounds");
}

比如，要插入 N00 节点时，需要更新默克尔树的根节点值，只需要在计算 N11 节点时获取 zeros(0) 的值来进行构建，然后在计算 root 的值时获取 zeros(1) 的值即可完成根节点的更新。

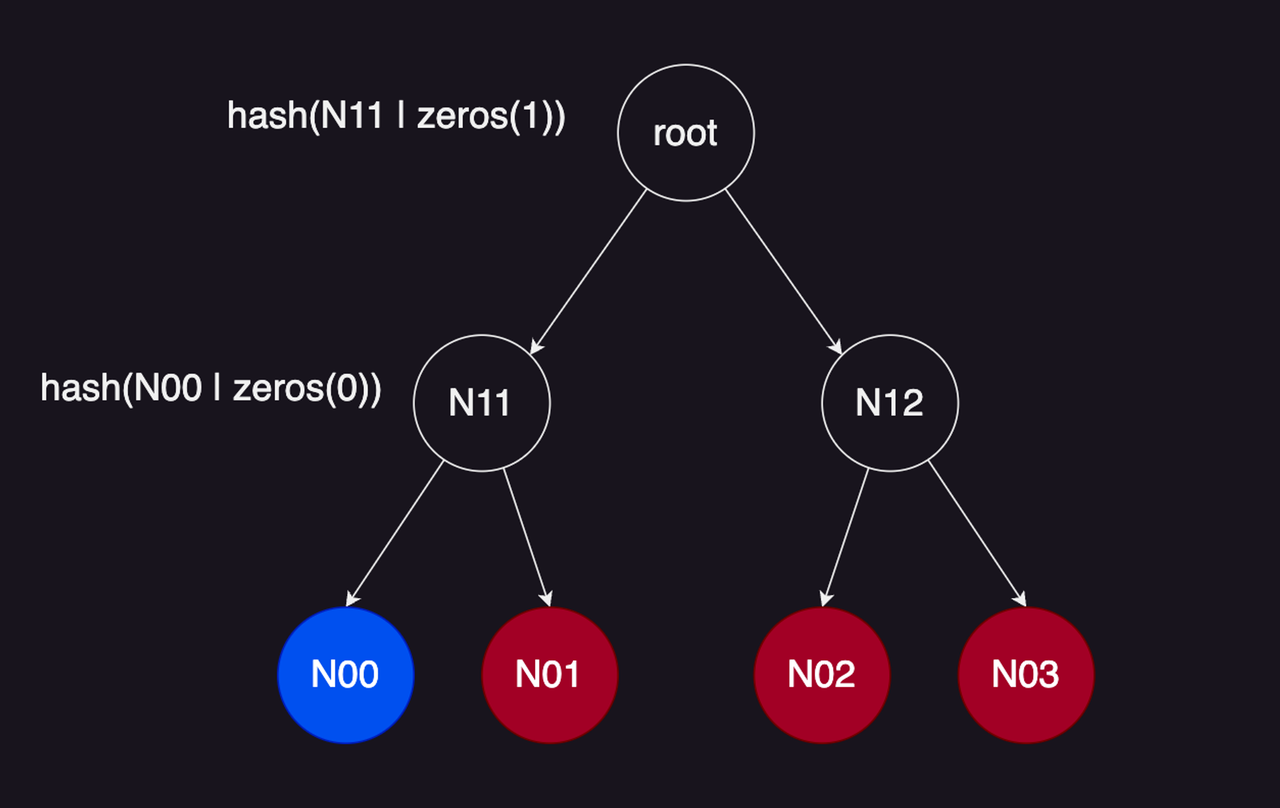
filledSubtrees 不是存放全被使用的子树根节点吗？

当 filledSubtrees[i] 被记录的时候是作为每个层级中最新更新的子树根节点，进行记录。被记录到 filledSubtrees 映射的时候该子树未必所有叶子节点都被使用了。

而只有当 filledSubtrees[i] 成为了当前层级所有叶子节点都被使用了的子树所对应的子树根时，它才会被使用。

请看案例：

当插入 N00 节点时， filledSubtrees[1] 的值将会更新，但此时它对应的子树 N11 还不是一个全部填充的子树。

而当插入了 N01 时， filledSubtrees[1] 的值会被更新为 N11 的值。

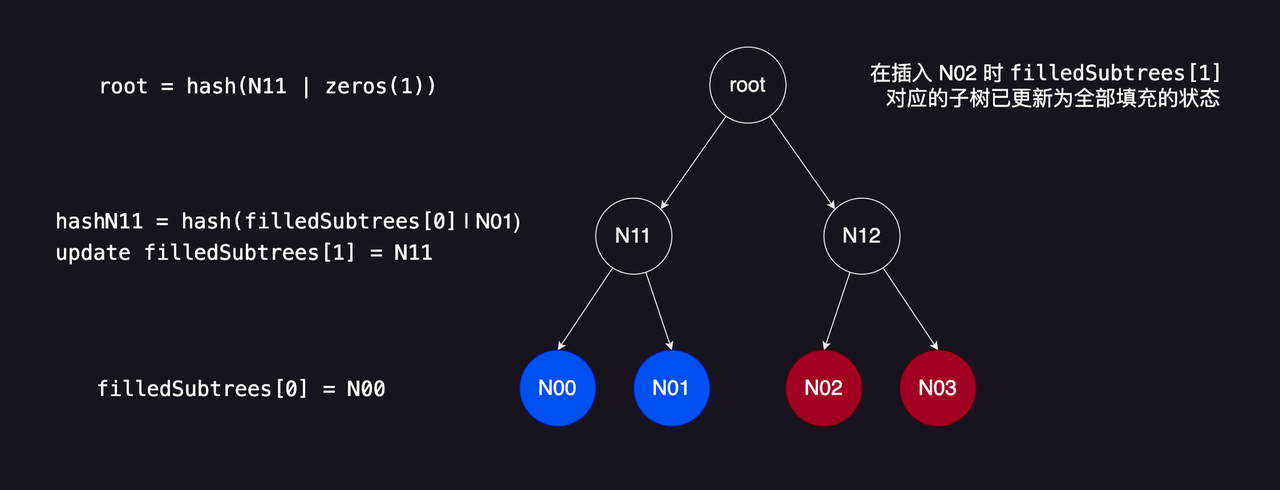
然后插入 N02 ， filledSubtrees[1] 的值将会被使用，此时它对应的子树已经是一个完全填充的子树了。

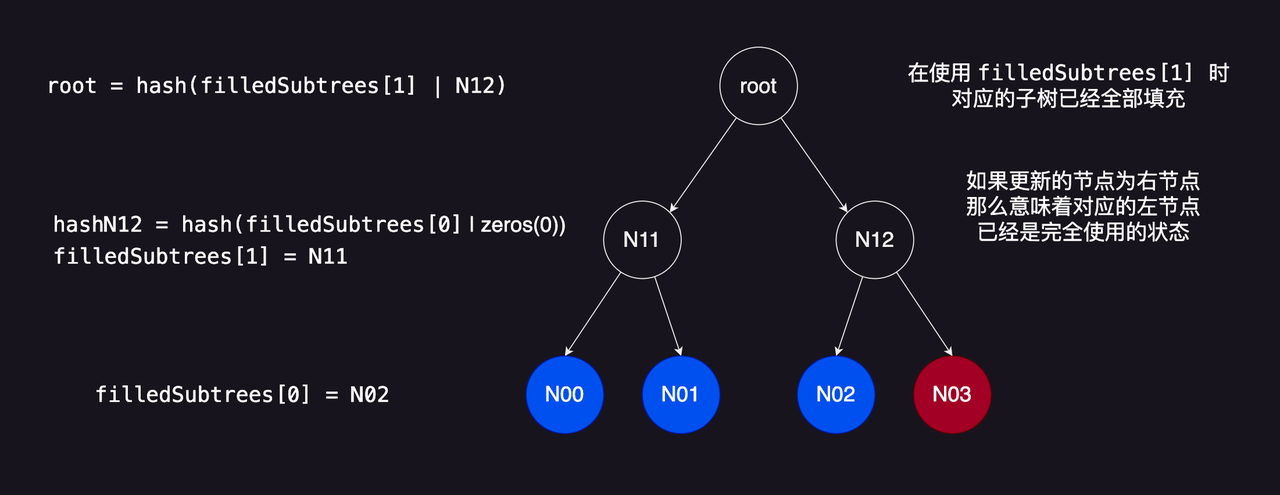
MerkleTreeWithHistory._insert() 函数插入叶子节点

MerkleTreeWithHistory._insert 函数

首先获取下一个插入的叶子结点索引，确保 Merkle 树未满，可以执行插入操作。
然后遍历更新 Merkle 树每一层相关的节点
1. 如果 currentIndex 是偶数，表示当前更新的节点为左节点，将当前哈希值存为左子节点，并将对应层级的默认右子节点（zero value）取出。（由于叶子节点插入是从左到右，所以当更新的节点为左节点时，右节点为空子树）。将第 i 层的 filledSubtrees 记录为当前哈希值。
2. 如果 currentIndex 是奇数，表示当前更新的节点为右节点，将左子节点（之前存储在 filledSubtrees 中的）和当前哈希值组合。（更新的节点为右节点，意味着对应的左节点已经是完全使用的状态）
3. 使用 hashLeftRight 函数计算当前层的新哈希值。
4. currentIndex 通过除以 2 得到父节点属于左子节点还是右子节点。
计算新的 root 索引，使用循环数组的方式避免超出 ROOT_HISTORY_SIZE 。
更新 currentRootIndex 。
把新的跟哈希存放在 roots[newRootIndex] 中。
更新 nextIndex
返回当前的叶子节点索引。

function _insert(bytes32 _leaf) internal returns (uint32 index) {
  uint32 _nextIndex = nextIndex;
  require(_nextIndex != uint32(2)**levels, "Merkle tree is full. No more leaves can be added");
  uint32 currentIndex = _nextIndex;
  bytes32 currentLevelHash = _leaf;
  bytes32 left;
  bytes32 right;

  for (uint32 i = 0; i < levels; i++) {
    if (currentIndex % 2 == 0) {
      left = currentLevelHash;
      right = zeros(i);
      filledSubtrees[i] = currentLevelHash;
    } else {
      left = filledSubtrees[i];
      right = currentLevelHash;
    }
    currentLevelHash = hashLeftRight(hasher, left, right);
    currentIndex /= 2;
  }

  uint32 newRootIndex = (currentRootIndex + 1) % ROOT_HISTORY_SIZE;
  currentRootIndex = newRootIndex;
  roots[newRootIndex] = currentLevelHash;
  nextIndex = _nextIndex + 1;
  return _nextIndex;
}

MiMC 哈希函数

hashLeftRight 函数使用 MiMC 哈希算法对两个树叶节点进行哈希。其中 _hasher 合约对应的是 Hasher.sol 。由于 MiMC 算法是由字节码编写的（甚至都不是用内联汇编写的），所以在 etherscan 上的是没有验证的状态。为什么不用内联汇编实现，开发者给的原因是：内联汇编不允许使用指令对堆栈进行操作。

MiMC 哈希算法： https://byt3bit.github.io/primesym/mimc/

MiMCSponge(R, C) 函数中

输入： R 是被哈希的信息， C 是轮常数。
输出： R 是哈希后的信息， C 是更新后的轮常数。

在对左叶子节点进行了第一次哈希操作后，需要对返回值进行相加取模操作 R = addmod(R, uint256(_right), FIELD_SIZE); ，以确保结果落在 FIELD_SIZE 范围内，以便将其作为输入再次进行哈希操作。

function hashLeftRight(
  IHasher _hasher,
  bytes32 _left,
  bytes32 _right
) public pure returns (bytes32) {
  require(uint256(_left) < FIELD_SIZE, "_left should be inside the field");
  require(uint256(_right) < FIELD_SIZE, "_right should be inside the field");
  uint256 R = uint256(_left);
  uint256 C = 0;
  (R, C) = _hasher.MiMCSponge(R, C);
  R = addmod(R, uint256(_right), FIELD_SIZE);
  (R, C) = _hasher.MiMCSponge(R, C);
  return bytes32(R);
}

在查找资料的过程中，发现了一个用 solidity 实现的 MiMC 算法，不知道是否和 Tornado 用字节码编写的算法版本细节一致，但是出于学习的目的可以对 solidity 版本的算法进行分享。

MiMC Solidity： https://gist.github.com/poma/5adb51d49057d0a0edad2cbd12945ac4#file-mimc-sol

整个算法主要由 220 轮的运算组成，每轮运算细节如下：

t 等于 xL 加上一个常数（注意这个常数每轮都不一样）取模
xR 等于上一轮的 xL
xL 等于上一轮的 xR 加上 t 五次方取模

pragma solidity ^0.5.8;

contract MiMC {
  uint constant FIELD_SIZE = 21888242871839275222246405745257275088548364400416034343698204186575808495617;

  function MiMCSponge(uint256 xL, uint256 xR) public pure returns (uint256, uint256) {
    uint exp;
    uint t;
    uint xR_tmp;
    t = xL;
    exp = mulmod(t, t, FIELD_SIZE);
    exp = mulmod(exp, exp, FIELD_SIZE);
    exp = mulmod(exp, t, FIELD_SIZE);
    xR_tmp = xR;
    xR = xL;
    xL = addmod(xR_tmp, exp, FIELD_SIZE);

    t = addmod(xL, 7120861356467848435263064379192047478074060781135320967663101236819528304084, FIELD_SIZE);
    exp = mulmod(t, t, FIELD_SIZE);
    exp = mulmod(exp, exp, FIELD_SIZE);
    exp = mulmod(exp, t, FIELD_SIZE);
    xR_tmp = xR;
    xR = xL;
    xL = addmod(xR_tmp, exp, FIELD_SIZE);

    ...
    // totally 220 rounds
    ...

    t = xL;
    exp = mulmod(t, t, FIELD_SIZE);
    exp = mulmod(exp, exp, FIELD_SIZE);
    exp = mulmod(exp, t, FIELD_SIZE);
    xR = addmod(xR, exp, FIELD_SIZE);

    return (xL, xR);
  }

  function hashLeftRight(uint256 _left, uint256 _right) public pure returns (uint256) {
    uint256 R = _left;
    uint256 C = 0;
    (R, C) = MiMCSponge(R, C);
    R = addmod(R, uint256(_right), FIELD_SIZE);
    (R, C) = MiMCSponge(R, C);
    return R;
  }
}

取款业务代码分析

当用户需要进行取款操作时，先向 Dapp 提供存款时获得的 note，再由 Dapp 补充一些相关的公共数据作为输入参数，然后就可以调用智能合约进行取款操作了。

整个 withdraw 函数接收了一系列的参数，对参数进行了检查后，调用 verifier.verifyProof 函数检验零知识证明的有效性（重点）。随后记录这笔取款，向收款地址发送取款金额。

为了文章的连贯性，参数检查部分将会在后面展开介绍

  function withdraw(
    bytes calldata _proof,
    bytes32 _root,
    bytes32 _nullifierHash,
    address payable _recipient,
    address payable _relayer,
    uint256 _fee,
    uint256 _refund
  ) external payable nonReentrant {
    require(_fee <= denomination, "Fee exceeds transfer value");
    require(!nullifierHashes[_nullifierHash], "The note has been already spent");
    require(isKnownRoot(_root), "Cannot find your merkle root"); // Make sure to use a recent one
    require(
      verifier.verifyProof(
        _proof,
        [uint256(_root), uint256(_nullifierHash), uint256(_recipient), uint256(_relayer), _fee, _refund]
      ),
      "Invalid withdraw proof"
    );

    nullifierHashes[_nullifierHash] = true;
    _processWithdraw(_recipient, _relayer, _fee, _refund);
    emit Withdrawal(_recipient, _nullifierHash, _relayer, _fee);
  }

首先来看一下输入参数：

_proof ：一个 zk-SNARKs 证明，用于验证与提款请求相关的所有条件和数据都是有效的
_root ：Merkle 树的根哈希值
_nullifierHash ：防止双重支付的标识符，当存款被提取时对应的 nullifier 将被标记为已使用
_recipient ：接收资金的地址
_relayer ：中继者地址，代替用户进行合约交互
_fee ：给中继者的费用
_refund ：交易的实际成本低于预支付的金额时，将退还给 _recipient 的金额

可以看到这些输入参数都在 verifier.verifyProof 函数被使用到， verifier 合约是根据约束电路生成的，用来验证零知识证明有效性的合约。由于他是根据约束电路生成的，所以其合约的具体实现我们不必深究，我们将重点放在约束电路的实现上。

通过阅读 withdraw.circom 的代码可以得知，其中 _proof 参数作为约束证明，而剩余的 6 个参数作为公共输入参与验证。

剩下的四个隐私输入，都可以通过 note 解析出来：

nullifier ：note 的前 31 个字节
secret ：note 的后 31 个字节
pathElements[levels] ：验证（nullifier + secret）为 Mercle 树中的子节点所对应的 proof path
pathIndices[levels] ： pathElements[levels] 中每个节点作为左子节点还是右子节点的标志位

template Withdraw(levels) {
    signal input root;
    signal input nullifierHash;
    signal input recipient; // not taking part in any computations
    signal input relayer;  // not taking part in any computations
    signal input fee;      // not taking part in any computations
    signal input refund;   // not taking part in any computations
    signal private input nullifier;
    signal private input secret;
    signal private input pathElements[levels];
    signal private input pathIndices[levels];

    ...

}

首先定义的了一个 CommitmentHasher() 组件 hasher ，其主要的功能就是哈希运算，根据输入的 nullifier 和 secret ，计算并输入 nullifierHash 和 commitment 。约束计算得到的 hasher.nullifierHash 和用户输入的 nullifierHash 需要是相等的。

    component hasher = CommitmentHasher();
    hasher.nullifier <== nullifier;
    hasher.secret <== secret;
    hasher.nullifierHash === nullifierHash;

然后定义的了一个 MerkleTreeChecker() 组件 tree ，用作验证 hasher.commitment 是否为以 root 为根的 Merkle 树中的一个叶子节点。

    component tree = MerkleTreeChecker(levels);
    tree.leaf <== hasher.commitment;
    tree.root <== root;
    for (var i = 0; i < levels; i++) {
        tree.pathElements[i] <== pathElements[i];
        tree.pathIndices[i] <== pathIndices[i];
    }

最后这部分代码，通过计算 recipient , relayer , fee , refund 的平方，间接地将这些值纳入到电路的约束中。这样做的目的，是为了将 Tornado.withdraw 函数中的输入 proof 和剩余的输入对应起来，避免了交易信息广播后，攻击者获取了 proof 以后将 recipient 等参数替换成自己的地址进行抢跑操作。将下列参数写进电路约束中后，一但 recipient , relayer , fee , refund 的值发生了改变，那么对应的 proof 也会改变，从而避免了在合约调用层面篡改参数的问题。

    signal recipientSquare;
    signal feeSquare;
    signal relayerSquare;
    signal refundSquare;
    recipientSquare <== recipient * recipient;
    feeSquare <== fee * fee;
    relayerSquare <== relayer * relayer;
    refundSquare <== refund * refund;

`MerkleTreeChecker` 函数检查

进入到 merkleTree.MerkleTreeChecker 函数，这个函数的功能就是约束 leaf 作为 root 的一个叶子结点。其中 DualMux() 函数的作用就是根据标志位 s 来决定 in[0] 和 in[1] 谁作为左子树谁作为右子树。

在决定了左右子树以后，将它们传入到 HashLeftRight() 函数中进行哈希操作，输出 hash 。不断地进行循环计算，并将最终结果和 root 参数进行约束 root === hashers[levels - 1].hash; ，确保两个值相等。

template MerkleTreeChecker(levels) {
    signal input leaf;
    signal input root;
    signal input pathElements[levels];
    signal input pathIndices[levels];

    component selectors[levels];
    component hashers[levels];

    for (var i = 0; i < levels; i++) {
        selectors[i] = DualMux();
        selectors[i].in[0] <== i == 0 ? leaf : hashers[i - 1].hash;
        selectors[i].in[1] <== pathElements[i];
        selectors[i].s <== pathIndices[i];

        hashers[i] = HashLeftRight();
        hashers[i].left <== selectors[i].out[0];
        hashers[i].right <== selectors[i].out[1];
    }

    root === hashers[levels - 1].hash;
}

DualMux() 函数的巧思

DualMux 函数是一个功能简单，但是有点巧思的函数，可以和大家分享一下。

首先是 s * (1 - s) === 0 约束，它限制了 s 的值只能是 0 或 1。

其次是输出的表达形式 out[0] <== (in[1] - in[0])*s + in[0]; ，这个写法不需要使用条件分支（ if … else … ），通过使用代数表达式来实现这种动态选择。

当 s = 0 时， (in[1] - in[0]) * 0 + in[0] = 0 + in[0] = in[0] ，因此 out[0] = in[0] 。
当 s = 1 时， (in[1] - in[0]) * 1 + in[0] = (in[1] - in[0]) + in[0] = in[1] ，因此 out[0] = in[1] 。

// if s == 0 returns [in[0], in[1]]
// if s == 1 returns [in[1], in[0]]
template DualMux() {
    signal input in[2];
    signal input s;
    signal output out[2];

    s * (1 - s) === 0
    out[0] <== (in[1] - in[0])*s + in[0];
    out[1] <== (in[0] - in[1])*s + in[1];
}

为什么 note 要采用 nullifier + secret 的形式

Tornado Cash 作为一个混币器，其功能是隐藏存款者与取款者之间的联系。采用 nullifier + secret 的形式来构成取款凭证 note 是为了防止多次重复取款的同时保护取款者身份不被泄露。

首先考虑只用 secret 的场景：

用户存款，生成 secret 值，并将其哈希值插入到 Merkle 树中；
用户取款，提供 secret 值对应的哈希进行验证；
验证通过，取款；
将改哈希值对应的取款状态置位 true，防止重复取款。

经过第 4 步操作后，取款者的身份和 secret 哈希对应上了，而 secret 哈希又和存款者的身份是对应的。这样就使得存款者和取款者联系上了，彻底暴露了资金链两端的联系。

采用 nullifier + secret 的形式可以解决上述的问题

用户存款，生成 nullifier + secret 值，并将其哈希值插入到 Merkle 树中；
用户取款，提供 hash(nullifier) 以及包含 nullifier 和 secret 的 proof 证明；
验证 proof
1. 验证 hash(nullifier) 和 proof 中的 hasher.nullifierHash 是否相等
2. 验证 proof 证明中的 hash(nullifier + secret) 是否为 Merkle 树的叶子结点
将 hash(nullifier) 对应的取款状态置位 true，防止重复取款。

通过这种形式，用户只需要暴露 hash(nullifier) 的值，其他人无法将 hash(nullifier) 和任意叶子节点 hash(nullifier + secret) 联

isKnownRoot() 函数检查 root 是否还有时效性

在 withdraw 函数中，会通过 isKnownRoot 函数对传入的根 _root 进行检查

require(isKnownRoot(_root), "Cannot find your merkle root"); // Make sure to use a recent one

在这个函数中，会使用到之前提到的全局变量

// 每次更新后 Merkle 树根的值
mapping(uint256 => bytes32) public roots;

// 可以存储的最大树根数量，避免存储过多的历史信息
uint32 public constant ROOT_HISTORY_SIZE = 30;

// 当前 Merkle 树根的值，代表处于 (currentRootIndex / ROOT_HISTORY_SIZE) 的位置。
uint32 public currentRootIndex = 0;

这个函数的功能就是检查传入的 _root 参数是否为 roots[] 中存储的最近的 ROOT_HISTORY_SIZE 个根。 roots[] 和 ROOT_HISTORY_SIZE 配合使用，实现了一个长度为 30 的循环数组，当前根的索引值为 currentRootIndex 。

function isKnownRoot(bytes32 _root) public view returns (bool) {
  if (_root == 0) {
    return false;
  }
  uint32 _currentRootIndex = currentRootIndex;
  uint32 i = _currentRootIndex;
  do {
    if (_root == roots[i]) {
      return true;
    }
    if (i == 0) {
      i = ROOT_HISTORY_SIZE;
    }
    i--;
  } while (i != _currentRootIndex);
  return false;
}

采取这个方案的好处：

避免了存储过多的历史根值，缩小了检索的范围。
采用最近的 30 个根值也能够避免当一个用户 A 生成了 proof 到调用合约取款这个时间区间内，另一个用户 B 发起了存款操作导致根值改变的情况。因为一但根值改变后，用户 A 的 proof 将无法通过校验。

参考文档

APP： https://tornado.ws/
Circuit Doc： https://docs.tornado.ws/circuits/core-deposit-circuit.html
Tornado Cash工作原理（面对开发人员的逐行解析）
真正的ZK应用：回看Tornado Cash的原理与业务逻辑

后记

也好久没有更新博客了，这段时间里处于一个对未来的职业发展以及技术积累比较迷茫的状态，导致做事情有点举棋不定，不敢做也不知道怎么做。在这种状态下既没办法静下心来深入研究某个东西，也没有办法鼓起勇气去探索新的方向，总的来说就是两个字：内耗。
目前也没有想到什么好的办法能够走出当前这种局面，真的让人苦恼。

标签：游戏攻略