相关资料:
对于特定的游戏问题使用启发式算法可以取得比AI算法更好的表现
https://www.askforgametask.com/tutorial/machine-learning/ai-plays-tetris-with-cnn/
Using A.I. to DOMINATE NERDS in TETRIS
Machine Learning: AI Learns To Play Tetris with Convolutional Neural Network
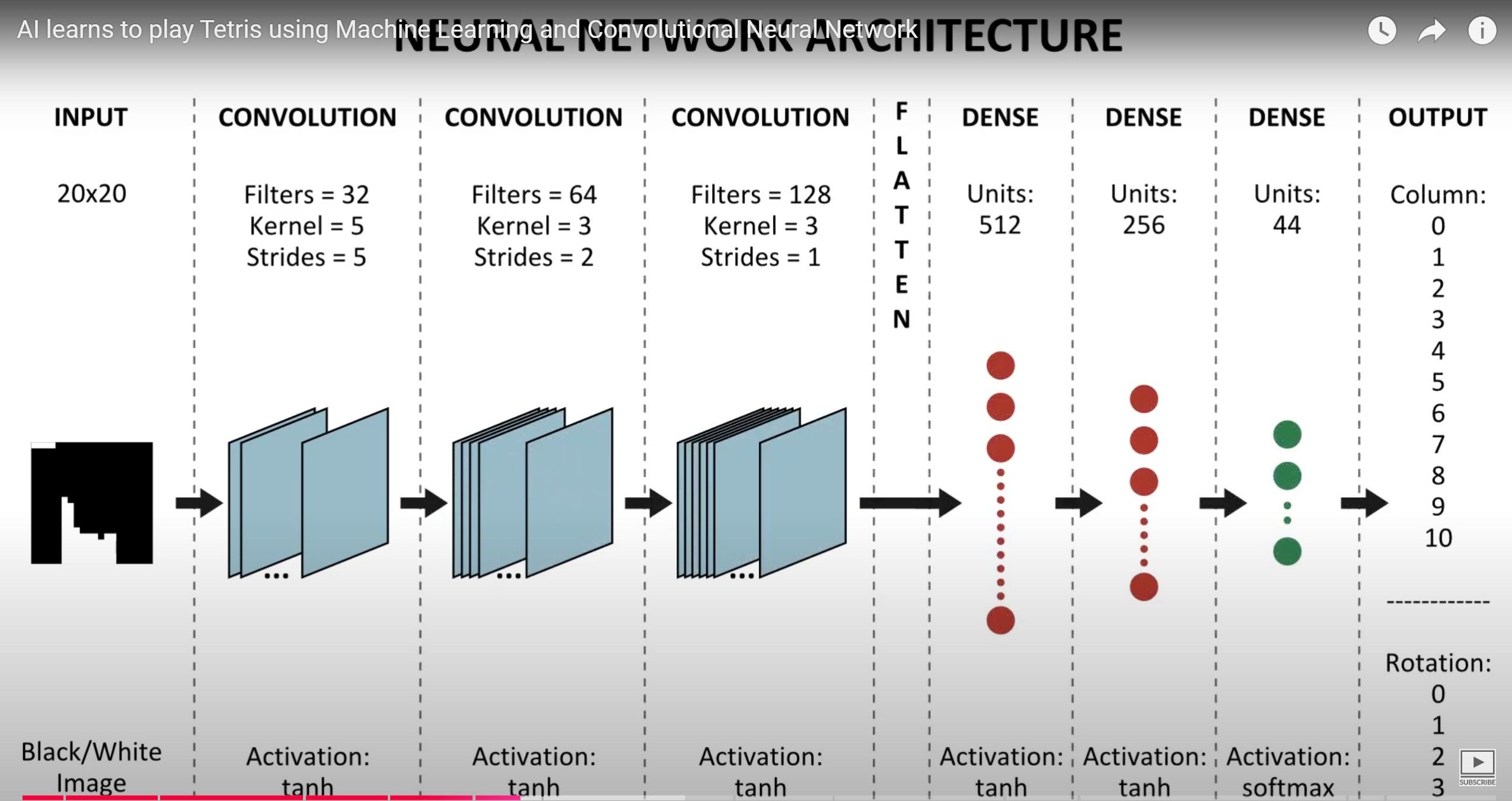
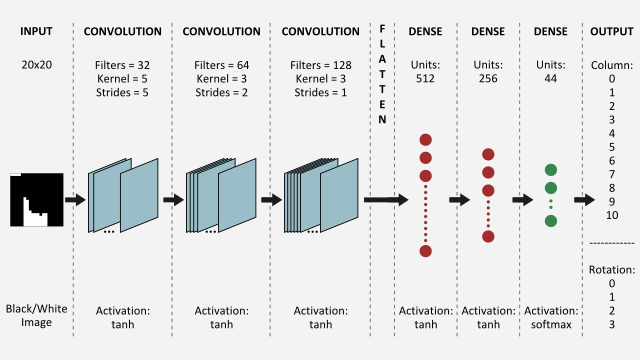
AI learns to play Tetris using Machine Learning and Convolutional Neural Network
A.I. Learns to Play Tetris
I Created An A.I. to DESTROY Tetris
前文( 对于特定的游戏问题使用启发式算法可以取得比AI算法更好的表现 )中讨论了解决俄罗斯方块的几种方法,不过由于只是介绍了大致的路线并没有给出足够的细节,因此也是很难进行真正的solution开发的,本文就是接着前文给出俄罗斯方块游戏的具体解决方法的细节。
就像前文所说的,对于俄罗斯方块游戏如果恰当的使用启发式算法往往可以获得比AI方法更好的解决效果,这就像之前分享的几篇如何解决 《2048》游戏的方法一样,可以说这里的《俄罗斯方块》和之前分享的《2048》游戏一样都属于较难解决的游戏问题,而且这两款游戏也同样属于难以直接使用通用的AI算法求解的游戏环境(不同于gym的atari游戏等等,解决方法需要定制化),也正是因为《俄罗斯方块》和《2048》游戏的具体解法需要定制化,因此分享一下这两款游戏的具体解法细节,关于《2048》游戏的解法和代码之前已经分享过了,本文则接续分享《俄罗斯方块》游戏的解法。
给出解法介绍之下定义一下《俄罗斯方块》游戏中的action空间,即可以操作的游戏动作有那些,这里为了下面介绍中出现歧义因此统一一下这部分概念;这里规定action有left,right,down,up四个按键动作,其中left和right代表控制当前的方块向左或向右移动,按键执行一次则当前方块移动一次;up按键代表方块的变形旋转,每个当前的积木块均有0度、90度、180度、270度这四种旋转角度,每按动一次up键当前下落的积木块都会顺时针旋转90度,即0度旋转为90度,90度旋转为180度,以此类推;由于每个时间步时当前积木都会自动下降一行,而按键down则意味在每个时间步时增加当前积木块的下降行,即在某个时间步按下down键后下落积木块会下降两个行,从而实现下落积木块的加速下落;为了描述简单这里再增加另一个动作就是all down,这个动作的本质就是down动作,不过这个all down意味着一直按down键直到当前下落积木块完成下落。
总结来说,left/right键代表着移动,up键代表着旋转90度,down键意味着加速下降(下降速度加倍)。
根据本文开头分享的几个 相关资料 可以知道现在的计算机解决《俄罗斯方块》游戏都有一个共同点,那就是计算机生成的执行动作序列大致为如下样式:
up, up, up, left, left, left, all down;
up, left, left, all down;
right, right, right, all down;
up, right, right, all down;
up, up, left, left, all down;
left, left, left, left, left, all down;
right, right, all down;
up, right, all down;
left, all down;
right all down;
而人类操作当前积木块下落的实际操作动作的序列情况可能是:
right, right, left, up, down, left, right, right
left, up, all down
right, right, right, right, left, up, up, left, up
up, left, left, right, right, left, up
left, left, up, right, right, up, left
可以看到,人类的操作东西的序列和计算机生成的操作动作序列有着明显的不同。人类的操作动作序列可以看做是一种不断的尝试的动作,在控制一个积木块下落的过程中时而向左移动,时而向右移动,时而旋转变换,时而再接着移动,而且人类控制过程中并不一定以all down动作结束,甚至人类可以在积木块与其他积木块贴合的同时控制积木块移动(这个动作估计玩过俄罗斯方块的都会懂),给出下面的两个示意图:
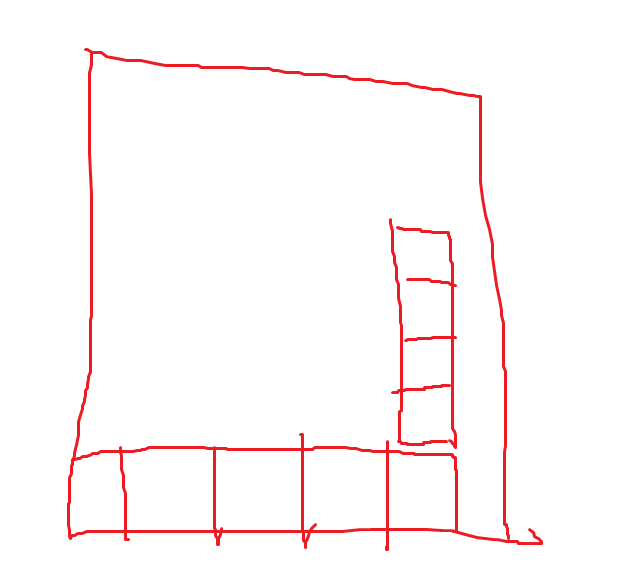
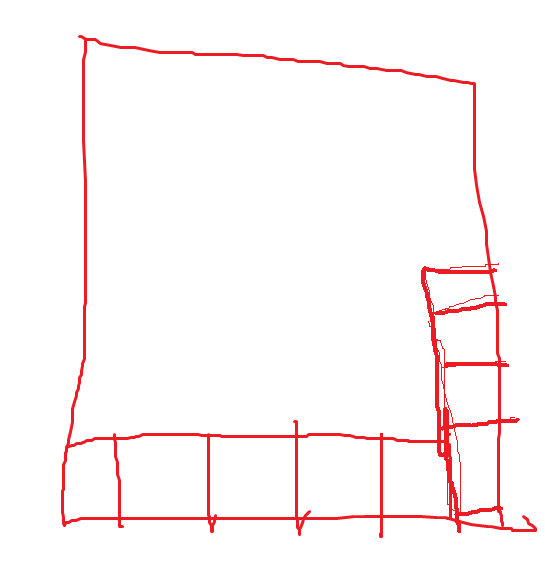
通过上面的两个示意图可以看到,人类控制积木块时可以在积木块和其他积木块贴合时依旧可以至少移动一次当前积木块(如果移动合法的话,比如向右移动式右侧不是紧靠墙),而这说明人类控制积木块的方式可以实现更加复杂的动作,以应对一下更加复杂的情景,比如在下面的场景下:
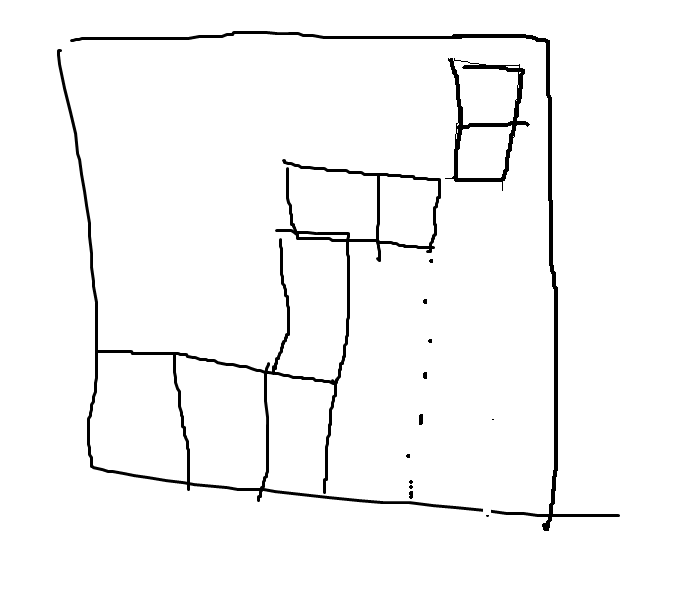
计算机程序生成的执行动作只能得到以下结果:
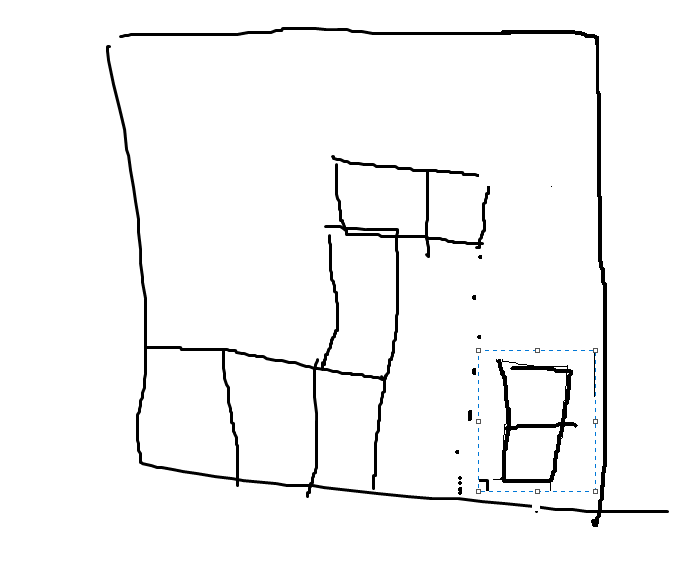
而人类的操作可以得到以下结果:
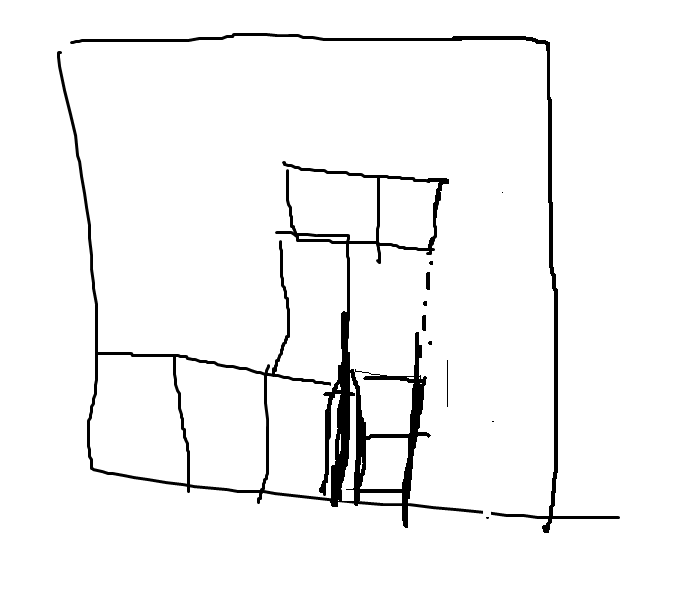
之所以人类操作和计算机生成的动作有这个区别的原因是现有的计算机程序解决俄罗斯方块都是根据当前的下降积木块和当前的已有积木块布局得到这个新积木块应该落在那个行上并且旋转角该是多少而不是直接获得具体的操作动作,也正因为计算机程序都是为当前下降积木块生成应该落地的列号和旋转角度这两个数值,然后再根据这两个数值生成具体的执行动作,因此才会有上面给出的如此不同的执行动作序列,也是因此所以计算机生成的执行动作都是先执行若干次旋转(包括0次),然后再只向左移动若干次或者只向右移动若干次,然后当下落积木块满足生成的下落列和旋转角后再最后执行all down动作以来加速完成积木块的下落。关于计算机程序解决俄罗斯方块问题时生成下落目标列和旋转角度的具体介绍可以参考 https://www.askforgametask.com/tutorial/machine-learning/ai-plays-tetris-with-cnn/ 。
之所以计算机程序设计生产下落目标列和旋转角度这两个数值而不是为每一时间步事实生成一个动作,其原因是如果为每个时间步生成一个动作难度极大,因为当前的已落地的积木块的情况和正在下落的积木块所组成的当前状态在相近的时间步中是极为相似的,而这会导致计算机程序难以编码来区分不同timestep下的具体状态,并且如果是使用AI程序的话如果为每个timestep生成一个action,那么这个问题就成了一个稀疏reward问题,而根据已有的相关研究(学术论文及俄罗斯方块解法的学术资料)可以知道如果是按照如此建模的话构建成稀疏reward后是更不利于算法训练和算法性能提高的。因此,计算机程序对俄罗斯方块问题的建模和解决都是计算当前下落积木块的目标落地行和旋转角度的,这部分的示意图如下:
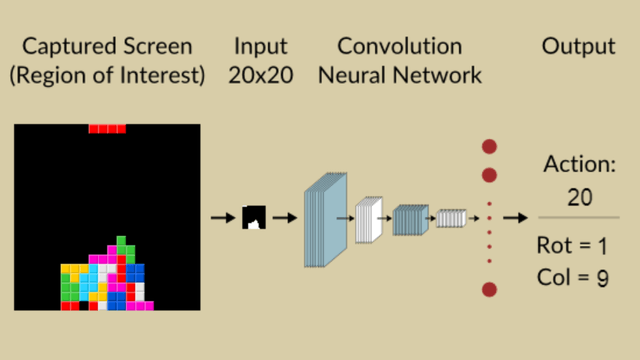
虽然几十年前的解决《俄罗斯方块》游戏的程序都是生成具体动作,而现在设计的计算机程序都是生成目标落地的行和旋转角度,虽然看似是简化问题甚至是有些偷工减料,但是根据相关的资料可以看到这种简化操作成功的避免了把该游戏的解法建模成一个稀疏reward的问题,极大的提高了算法的求解性能,当然由于现在的对于该游戏的计算机解法的这种生成目标落地的行和旋转角度会导致计算机程序无法实现人类操作的这种灵活性(无法在下降到某个行后旋转或再移动等复杂动作,并且如果某个空缺位置的正上方存在遮挡的情况也是直接将遮挡部分与空缺部分之间的部分考虑成不可填充的),但是这种设计(生成目标落地的行和旋转角度)会极大提高算法性能提高最终的算法得分,而对于中间空缺部分并且可以填补的情况毕竟在游戏中出现的比较小概率,而这时把该部分当做已填满部分也不会对算法性能有太多影响。
给出一个有空缺但是上方被遮挡的情况:

在这种情况下计算机程序生成的解决方法并不会通过最右侧的三个空缺格进入下方后进行填补,如:
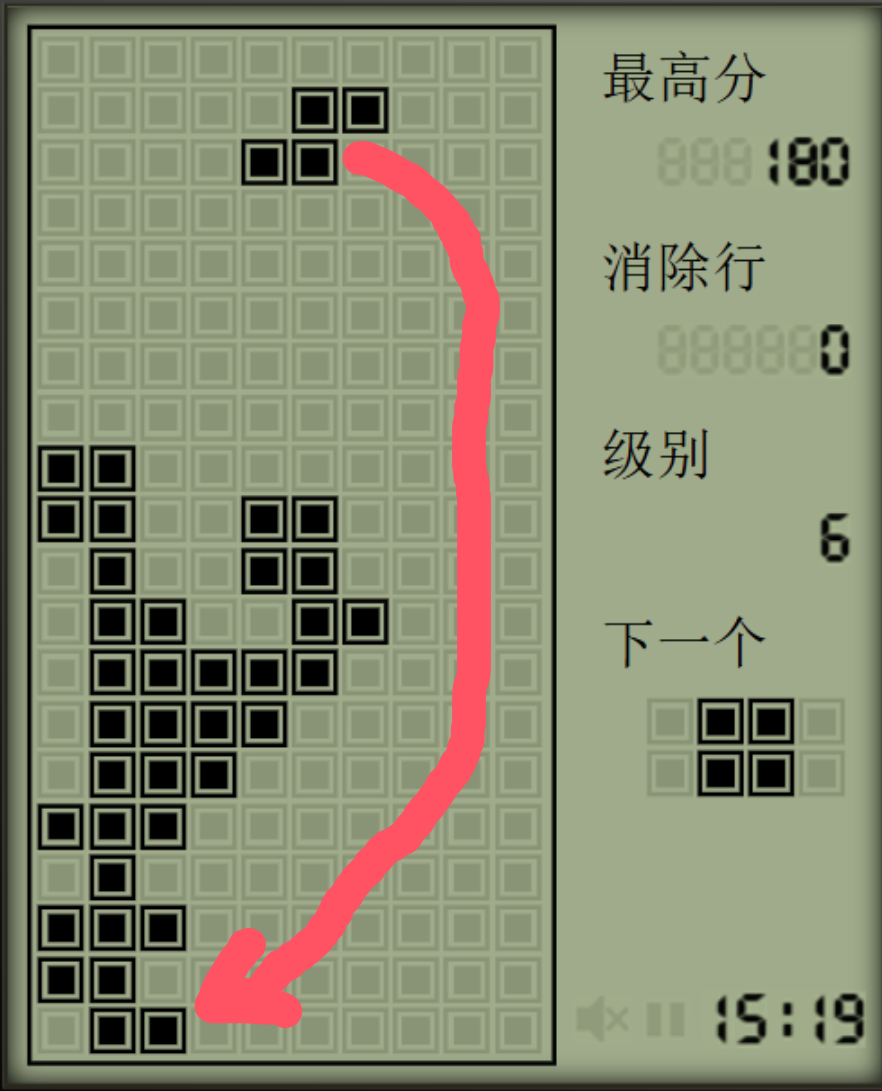
在计算机程序中这种情况等价于:

而计算机生成的最后操作的空间也是上图红框中最右侧的三列,可以说垂直有遮挡的空格在计算机程序中都被视为已填满的部分。
由于中间有空洞,上方被遮挡,甚至周围都被遮挡的情况下其实很多时候也无法利用当前下落积木对其进行操作的,如:

其中的中间空格也都是无法被直接操作的,因此这些空格可以当做已填满考虑,这样也不会对算法性能有什么影响,如下图中的红色圈中的部分,这些部分都是可以在计算机程序中当做已填满的。

正事因为这种不考虑被遮挡部分的空间的这种假设,最后算法生成的只有目标列和旋转角度,由此避免了难以训练的并且复杂的稀疏奖励建模问题,而得到了一个易于建模并且容易计算的问题建模。
在解决了问题建模后我们可以进行具体的算法设计部分了(下面的所有种类的计算机解法都是基于该问题的建模方式)。
在以上的建模方式下给出具体的解法:
- 规划法
- 遗传算法+规划法(遗传算法辅助规划法)
- 监督学习法
- 强化学习法(TD算法)
在进行具体的算法细节之下需要明确的是《俄罗斯方块》游戏中下落积木块和已落地积木块的游戏状态表示(这部分示意图图片来自: https://www.askforgametask.com/tutorial/machine-learning/ai-plays-tetris-with-cnn/ ),关于下落的积木块表示如下:
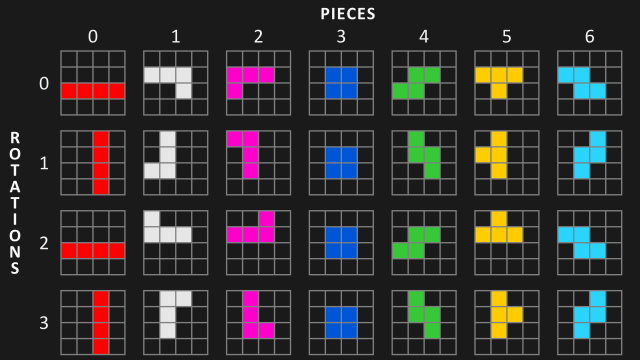
可以看到该游戏中共有七种积木块,每一种积木块均有4个旋转角度,因此在计算机算法控制积木块all down下落时共有4*7=28种形态的积木块。
关于棋牌我们需要知道在《俄罗斯方块》游戏中整个游戏盘面的布局是固定的,及高20,宽10的一个布局,使用np.array来表示可以为:
board=np.zeros((20, 10))
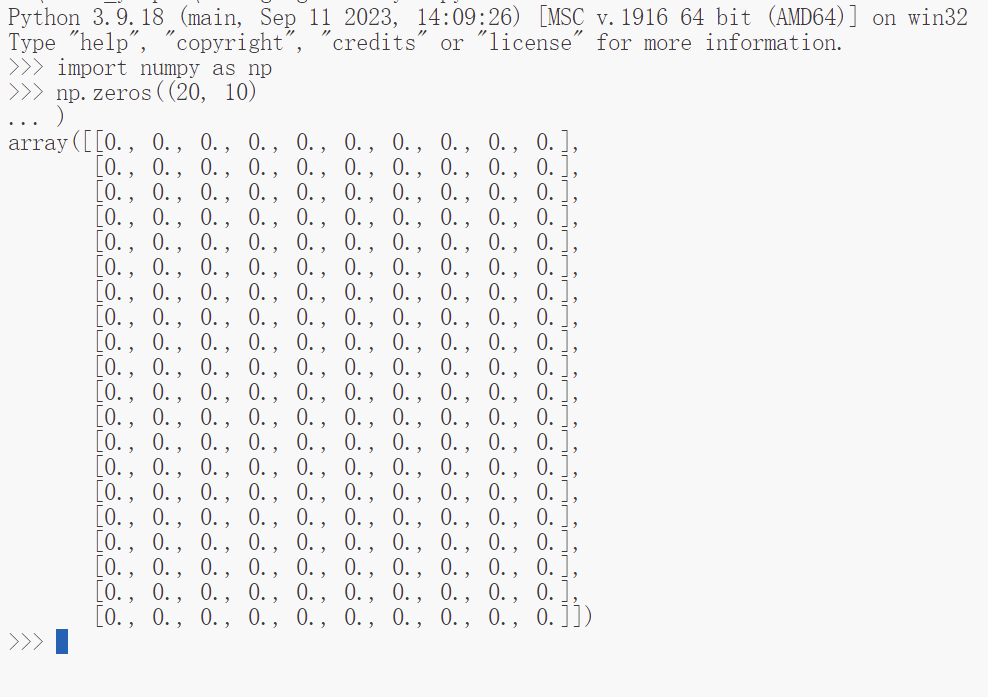
在知道了棋牌的棋面布局的状态表示和下落积木块的表示形式后需要知道这里所有的计算机求解程序其实都是一种有模型的求解方式,即所有解法都可以根据现有的棋面布局和下落积木块的形态来向前推演出执行某个动作后的棋面状态(或者说是当前下落积木块在确定落点所在列和旋转角度后下落停止后的棋面状态),这一点和AlphaGo下围棋时可以预先向前推演出未来下多少步棋后的棋面状态是一样的。
就个人的观点来看,将计算程序求解《俄罗斯方块》问题的输出从每一步的up,down,left,right改为输出下落目标列和旋转角度后最难的两个技术点就是下落积木块的状态表示和确定下落目标列和旋转角度后执行落子后棋牌的棋面布局的推演,在完成了这几样事情后我们就可以使用规划算法、遗传算法、强化学习算法来对其进行求解了。
使用“规划算法”求解
规划算法求解其实就是利用 效用理论 来评估最佳移动方式。它通过一系列启发式方法来衡量当前配置的一些特性,例如方块堆叠的高度或存在的空隙数量,这也看做是一种启发式算法。
这些启发式方法通过加权平均进行组合,在确定各个因素的权重系数后我们就可以获得不同棋牌状态的评估,这里给出的棋牌的评估为cost,也就是说值越大则状态评估越差,假设评估的因素为方块堆叠的高度 \(x\) 或存在的空隙数量 \(y\) ,cost函数为:
\(cost=w_1*x+w_2*y\)
注意,这里只是为说明之用,关于应该更全面的考虑的因素可以参考: 对于特定的游戏问题使用启发式算法可以取得比AI算法更好的表现
在一些公开资料中考虑的因素量为5个以上,包括棋牌布局的凹凸度,最高堆叠高度,最低的堆叠高度,等等,这里不过多讨论和分析规划法中的cost函数的因素个数。
在确定cost函数中的各因素权重系数后(这个系数可以看做是人为头脑风暴预设的,或者是人为手动调整的),那么在某个状态棋牌布局和当前下落积木块已知的情况下我们可以向前推演在指定的落点列和旋转角度后积木块落定后的棋盘布局及该状态下的棋牌布局的cost值,根据不同的下落积木块我们可以知道一共有多少可能,比如方形积木块,由于其长宽为2,旋转后依旧为方块,因此方块的下落可能共有10-2+1=9,因为棋牌宽为10,方形积木块长宽为2,因此才有9种可能的下落所在列,由此可以知道,在棋牌状态cost函数确定,并且可以推演出未来的几种棋牌状态及对应的cost后,我们就可以计算出哪个下落落点列及旋转角度所对应的cost函数越小,那么我们就执行对应的下落点所在列和旋转角度即可;这里依旧是假设方块,方块初始时所在的列为4号和5号列(棋牌宽为10, 10个列编号分别为0 9),那么下落的可能列分布为0 8(这里以下落块的最右侧列作为下落列的计算列),假设计算出最优的下落列为0,那么可以转换为具体的执行动作为left,left,left,left,all down;如果计算出最终的下落列为8,那么转换后的具体执行动作为right,right,right,right,all down。
使用规划算法时我们也可以很好的解决在知道当前下落块及下一个下落块(有些《俄罗斯方块》游戏中是可以看到下一个未来的下落块的形态的)的情况下进行计算,示意如下:
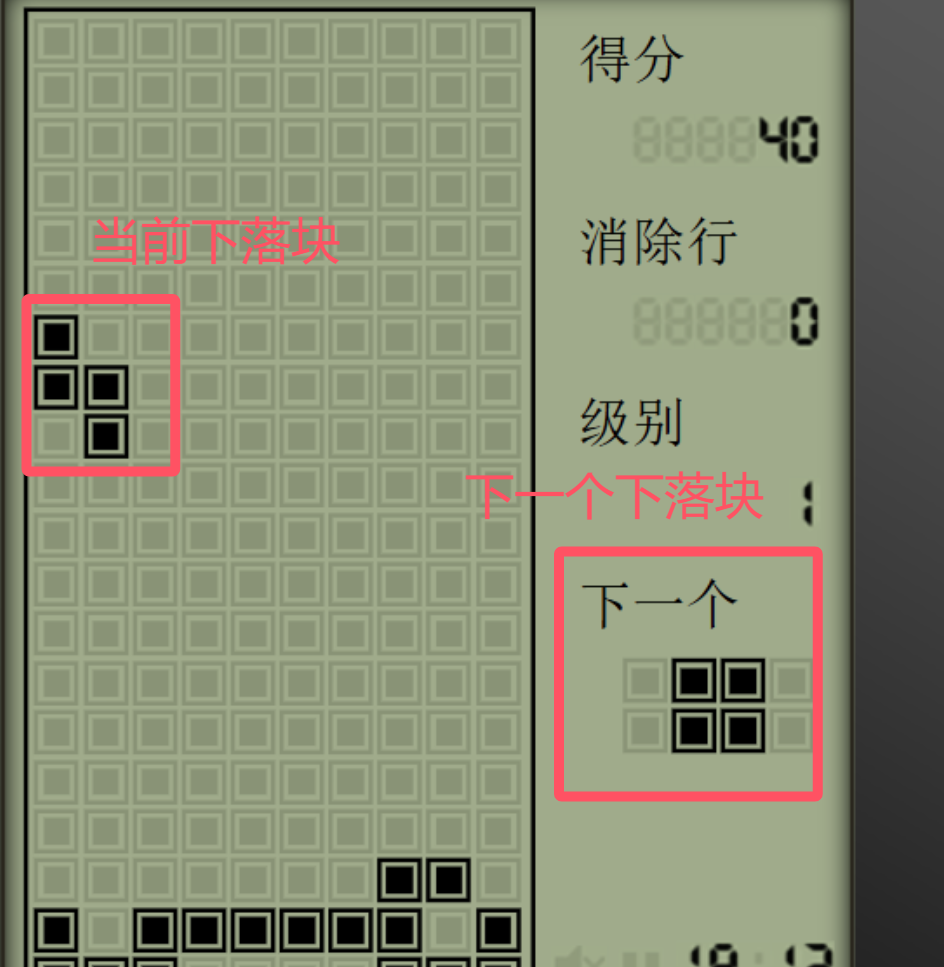
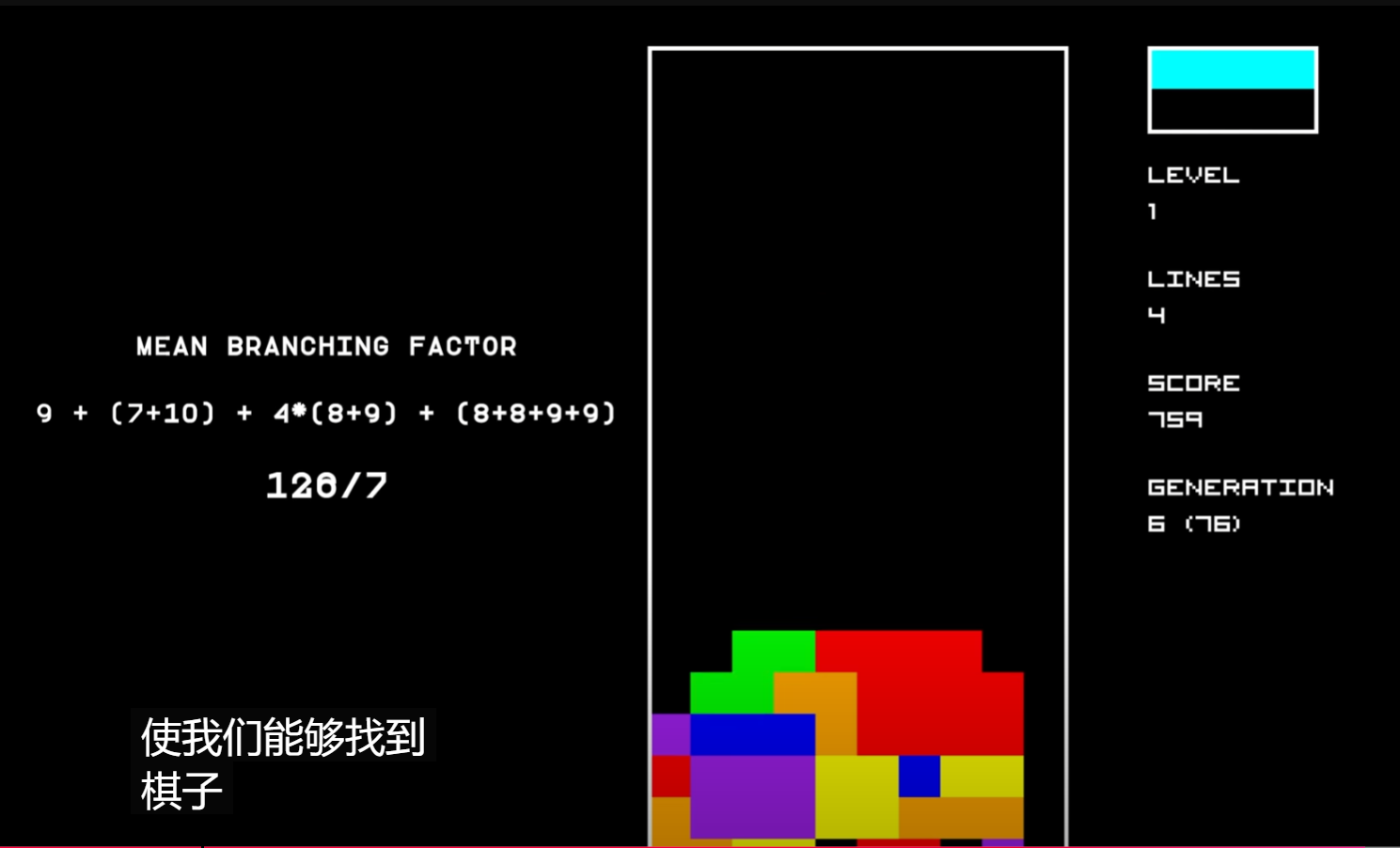
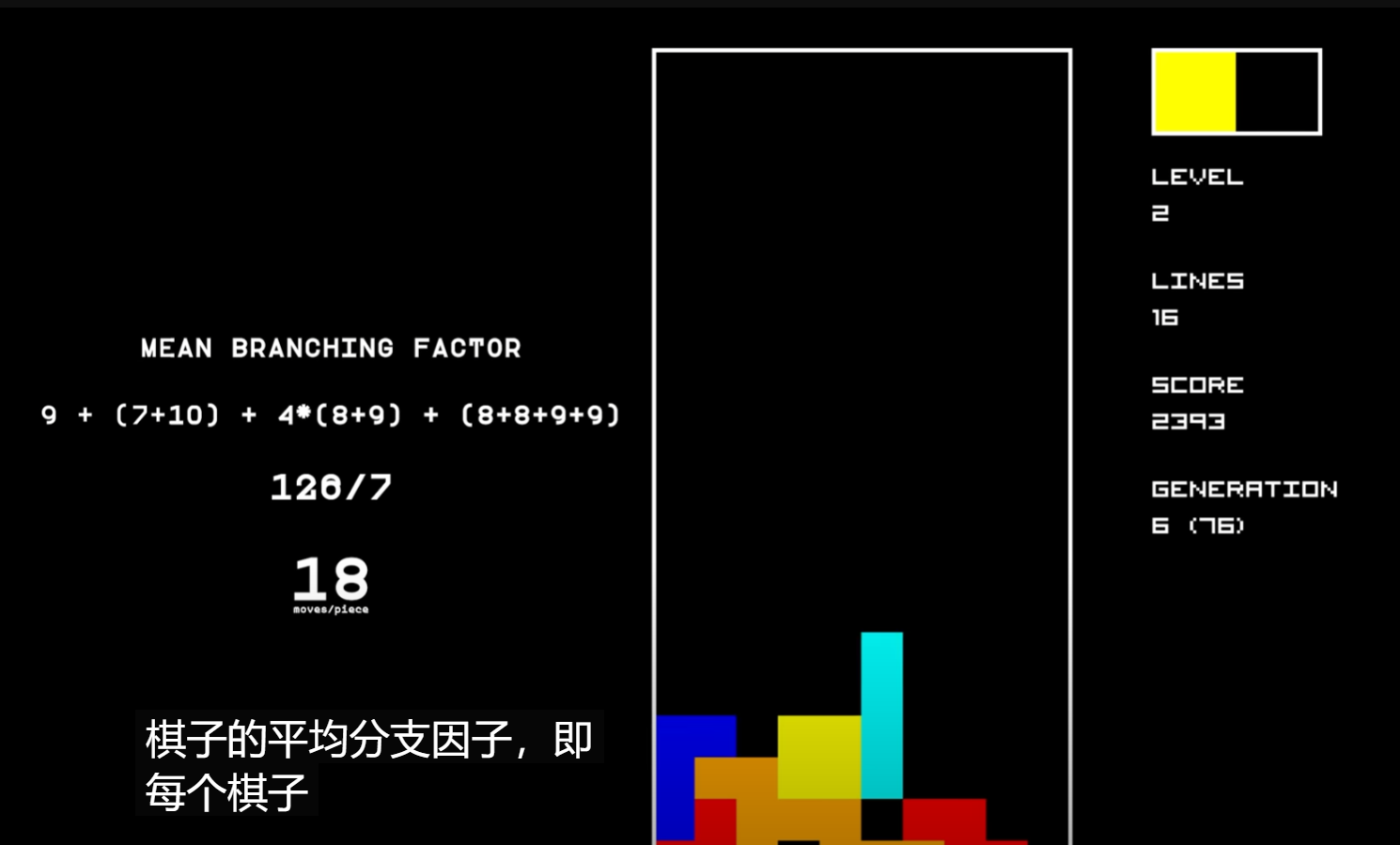
根据 https://www.youtube.com/watch?v=LGNiWRhuIoA 可以知道I型积木块横着的姿态下可以有7种下落的行,也就是有7种可能的落点(10-4+1=7, I型积木块长度为4),I型积木块竖着的姿态下有10种下落的落点(10-1+1=10, 竖着的情况下I型积木块宽为1),同理我们可以计算出7种积木块在4种旋转角度下共有多少种落点,具体如下:(方块积木块4种旋转角度下形状相同,因此落点只有一个姿态下的情况,同理I型的有两种)

经过计算我们可以知道这7种积木块一共可以有126个落点,平均为126/7=18。
根据以上的不同积木块的落点数,我们可以大致的计算出不同情况下规划算法需要计算cost的状态数。假设我们在使用规划算法时需要根据当前积木块和下个积木块落地的cost值来计算当前的积木块的下落点和旋转角度,那么当我们知道当前积木块和下个积木块的情况时我们大约平均存在 \(18*18=324\) 种可能的下一个状态,也就是需要规划算法计算大约324种下落后的棋牌状态;当我们知道只当前积木块的情况而不知道下一个积木块的情况时我们需要计算 \(18*1246=2268\) 种。当然这里的规划都是推演到连续两个积木块后的状态,并以此计算当前的积木块的最优下落选择的,我们同样也可以只计算推演一次积木块落地后的状态的,这就如同AlphaGo下围棋时需要前向推演几步一样,一般来说推演的步数越长其算法效果越好但也越消耗计算时长,这里建议的就是只计算一次积木块下落或两次积木块下落,否则对计算下落行和旋转角度的时间花费会难以接受的,而且由于这里的启发式算法所预先设定的cost函数的质量并不一定保证(因素种类和权重都是没有经过调优的),因此过长的推演step对算法提升不明显也没有太大意义。
遗传算法+规划法(遗传算法辅助规划法)
遗传算法+规划法(遗传算法辅助规划法)求解《俄罗斯方块》游戏其实和规划算法基本一致,唯一的不同是规划算法中cost函数中不同考虑因素的权重是人为凭借专家经验设定的(注意,这里使用的是学术术语,如果用白话解释的话就是人工手动试验出的权重值,就和做菜时放盐一样,多少全凭手感),但是由于人工设定权重往往需要花费大量的试验时间并且也难以保证会得到一个较为可靠的权重值,因此网上最为常见的解决方法则是在规划算法的基础之上使用遗传算法来优化这里的cost函数中的各因素权重。具体的操作步骤,将cost函数的各因素权重值编码为遗传算法中的基因型,而遗传算法中某个DNA个体的fitness则为该DNA表现(也就是某个cost函数下的各因素的权重)下形成的cost函数在规划算法下完成一整个游戏(玩到失败结束)的步数(或者叫做episode长度),由此来利用遗传算法来优化规划算法中的cost函数中的各因素的权重值,由此实现规划算法中的各因素权重从人为凭经验设定到使用遗传算法自动计算出的转变。注意,这里因为是使用遗传算法优化cost函数中各因素的权重,因此在遗传算法中种群个体的用来编码的cost函数中的各个因素的权重都是随机初始化的,并且使用遗传算法来寻找和优化规划算法中cost函数的各因素权重是极为耗费时间的,因为每次评估一个cost函数下权重值的好坏都是需要该cost函数下完整玩完一次游戏才可以进行,而当所有遗传算法中的种群个体都分别完成这样的一次评估才可以完成一次遗传算法的优化计算,根据网上的一些资料可以知道这个过程可能需要几天甚至几周的时间才能完成,这个时间可以和deep learning训练一个中型网络的时间匹敌了。
当然使用遗传算法优化好cost函数的各因素权重值后最终进行游戏求解的其实依旧是规划算法,而且当我们获得一个表现十分好的cost函数权重值后使用规划算法是可以取得比强化学习算法还要好的求解效果的。
这些启发式方法通过加权平均进行组合,并选择得分最高的配置作为下一步行动的依据。初始的权重是完全随机的,随后经过几代的进化算法不断优化。表现最佳的AI(即最佳的权重组合)被选为下一代的基础,并进行微小的突变调整。
你可以看到,最开始的AI几乎是随机操作的,但经过几代后,其表现迅速提升。
这里展示的是50代的试错过程。实际上,我已经运行了好几天,但目前遇到瓶颈,因为AI已经足够优秀,每场游戏都能持续数百万次操作,这需要 数小时 才能完成一场游戏!
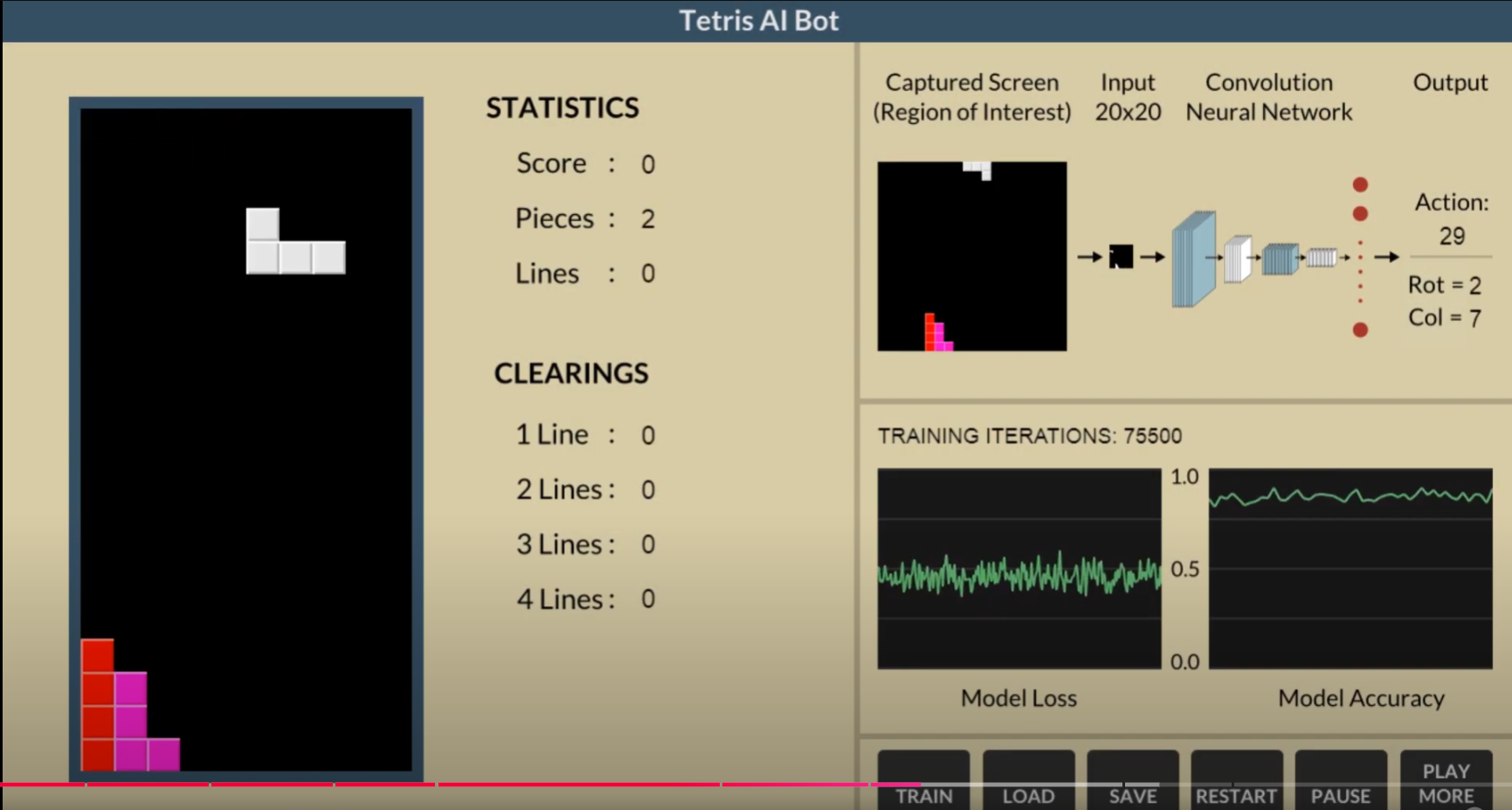
俄罗斯方块游戏的一个演示地址:
https://www.askforgametask.com/html5/tutorials/tetris_ai_bot/source/
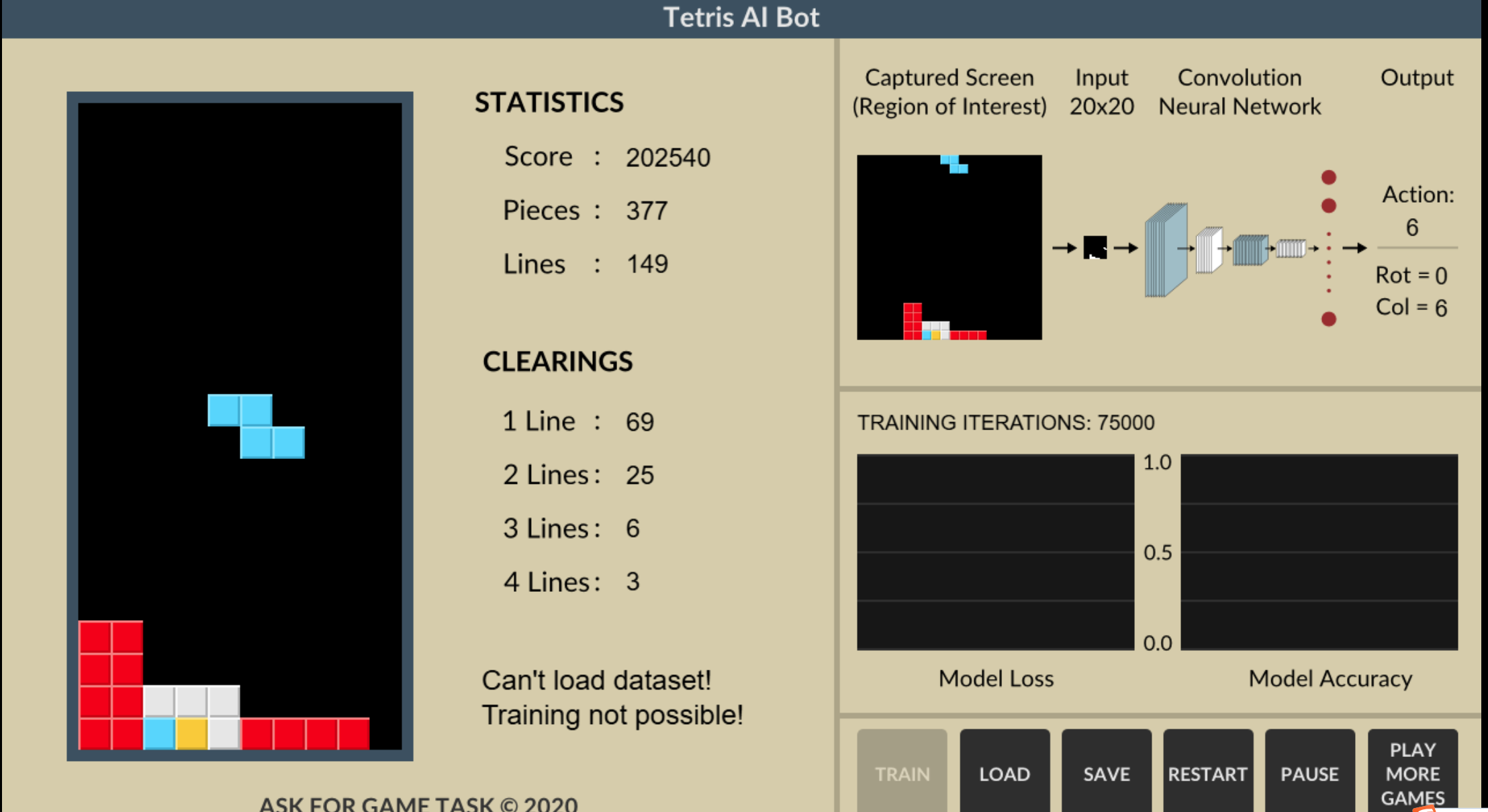
《俄罗斯方块》游戏试玩在线地址:
http://123.geiwosou.net/game/tetris/
强化学习算法library库:(集成库)
https://github.com/Denys88/rl_games
https://github.com/Domattee/gymTouch
个人github博客地址:
https://devilmaycry812839668.github.io/
标签:游戏攻略








